Table of Contents

Chaussette

To improve my skills in mastering the symbolic execution framework, I tried to solve this challenge with as many means as possible.

I skipped the first reversing part which is not the interest here.

Introduction about the challenge

The goal of the challenge is to solve a lot of “puzzle”, which consist of a entry of arguments (RDI and RSI (System V ABI x86_64 calling convention)).

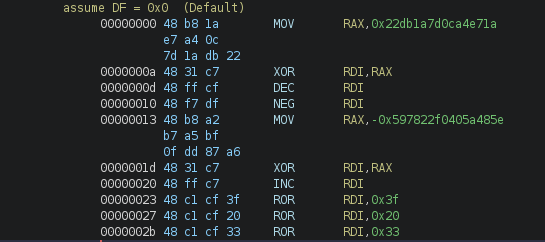
overview

The goal is to find input when RAX==0 at the end of the shellcode.

Using the miasm Symbolic Execution Engine

The “classic” way is to go through the intermediate representation of the shellcode, then to symbolize the elements of the intermediate representation, (we apply an “ir lifting”), we then try to resolve the expression associated with RAX to find the unknowns (in our case RDI and RSI), then, print them all.

from miasm.analysis.machine import Machine
from miasm.core.locationdb import LocationDB
from miasm.analysis.binary import Container
from miasm.expression.expression import *
from miasm.ir.symbexec import SymbolicExecutionEngine
from miasm.ir.translators.z3_ir import TranslatorZ3
from miasm.analysis.simplifier import *
from z3 import *


def solve_shellcode(shellcode, startaddr):
    loc_db = LocationDB()

    container = Container.from_string(shellcode, loc_db)
    machine = Machine('x86_64')
    lifter = machine.lifter(loc_db)
    dis_engine = machine.dis_engine(container.bin_stream, loc_db=loc_db)



    ##  add the block (the one) to the ircfg    ##
    current_blk = dis_engine.dis_block(startaddr) 
    ircfg = lifter.new_ircfg()
    lifter.add_asmblock_to_ircfg(current_blk, ircfg)
    init_state = {}
    ##
    
    ##  Symbolize the registers ##
    init_state[ExprId("RDI", 64)] = ExprId('input_RDI', 64)
    init_state[ExprId("RSI", 64)] = ExprId('input_RSI', 64)
    ##
    
    ##  Launch the Symbolic execution engine    ##
    sb = SymbolicExecutionEngine(lifter, state=init_state)
    sb.run_at(ircfg, addr=startaddr)
    
    print(sb.dump()) # dump the state, each register / memory referenced is now symbolized into a expression
    ##
    
    ##  Now we have a expression, we can now try to solve it using z3   ##
    trans = TranslatorZ3(loc_db=loc_db)
    s = Solver()
    expr_out = sb.eval_expr(ExprId('RAX', 64))
    s.add(trans.from_expr(expr_out) == trans.from_expr(ExprInt(0, 64))) # the value I want 
    ##
    
    if s.check() == sat: # if satisfiable
        model = s.model()
        for i, _ in enumerate(model):
            print(_,":", hex((model[_].as_long()))) # parse the model

    else:
        print("No solution found.")
        exit(1)


shellcode = open("shellcode.bin", "rb").read()
solve_shellcode(shellcode,0)

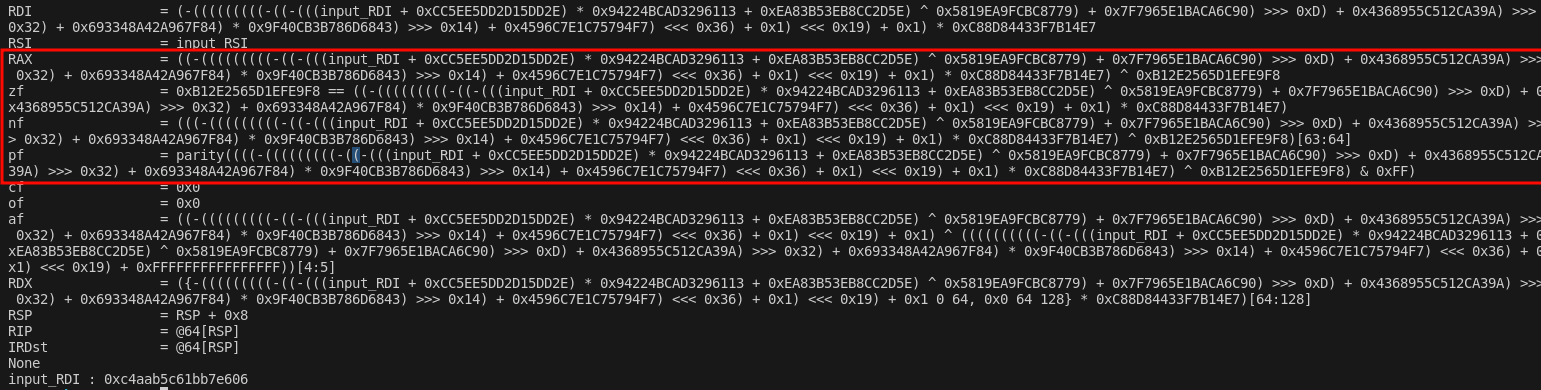
(In this example only RDI is used in the RAX expression) ghidra1

So this works well, but the challenge is harder than that, the shellcode becoming bigger and bigger takes z3 in a very thorny situation, my RAM cannot make it to the final level.

The Triton Framework

Triton is a DSE Engine (Dynamic Symbolic Execution Engine). The work process of a DSE Engine and a “SE” Engine are different, when the Symolic execution engine is looking statically the code, the DSE is working by executing the instruction, not by reading the entire flow. This is very handy to minimise the Path Explosion in statically compiled binary, in some obfuscation situation and a lot more. In plain world, I can very easily choose what to symbolise because i’m choosing what should i execute.

In this case, using a DSE or a SE is the same, BUT triton involves an another SMT solver, with better performances. BitWuzla

It’s possible to just send the previous miasm expression to bitwuzla, but it’s time to learn how to use Triton.

from triton import *

def DSE_code(code, startaddr=0x1000):
    ctx = TritonContext(ARCH.X86_64) # choosing the architecture
    ctx.setSolver(SOLVER.BITWUZLA) # choosing the solver (important)
    ctx.setConcreteMemoryAreaValue(startaddr, code) # write the shellcode where we want

    # ctx.concretizeAllMemory()
    # ctx.concretizeAllRegister()

    ##  reduce and optimisation flags   ##
    ## thanks to Deadc0de for the tips
    ctx.setMode(MODE.ALIGNED_MEMORY, True)   # optimisation
    ctx.setMode(MODE.CONSTANT_FOLDING, True) # reduce expressions
    ctx.setMode(MODE.AST_OPTIMIZATIONS,True) # reduce ast depth with arithmetic

    ## Same as preview, symbolize the registers ##
    ctx.setConcreteRegisterValue(ctx.registers.rip, startaddr)
    ctx.symbolizeRegister(ctx.registers.rdi, 'inputRDI')
    ctx.symbolizeRegister(ctx.registers.rsi, 'inputRSI')
    
    pc = ctx.getConcreteRegisterValue(ctx.registers.rip)
    count = 0


    while pc:
        # Fetch opcodes
        opcodes = ctx.getConcreteMemoryAreaValue(pc, 16)

        # Create the Triton instruction
        instruction = Instruction(pc, opcodes)
        if ctx.processing(instruction) == EXCEPTION.FAULT_UD:
            print(f"[-] Instruction is not supported: {instruction}")
            break

        count += 1
        print(instruction)

        pc = ctx.getConcreteRegisterValue(ctx.registers.rip)

    ast = ctx.getAstContext()

    ##  Get the expression of rax and ask for expression==0 
    expr = ast.equal(ctx.getSymbolicRegister(ctx.registers.rax).getAst(), ast.bv(0,64))
    model = ctx.getModel(expr) # BITWUZLA IN ACTION
    print(model)
    t = {}
    for i, _ in enumerate(model):
        # print(model[0].getVariable())
        # print(model[0].getValue())
        t[str(model[i].getVariable()).replace(":64","")] = int(model[i].getValue())
    return t

And now we are able to solve the challenge, after a veryyyy long time. (couple of hours).

registres = {}
registres["inputRDI"] = 9243637858070793867
registres["inputRSI"] = 0

shellcode = b''
p = pwn.connect("127.0.0.1", "4000")# https://hackropole.fr/fr/challenges/reverse/fcsc2023-reverse-chaussette/

while True:
    p.send(pwn.p64(registres["inputRDI"]))
    p.send(pwn.p64(registres["inputRSI"]))
    taille =  int.from_bytes(p.recv(8), byteorder='little', signed=True)
    if(taille == 0 or taille == -1):
        print("STOP ! (break -1) (hope its flag)")
        break
    while(len(shellcode)<taille):
        shellcode = shellcode+p.recv(0x1000)
    d = DSE_code(shellcode)
    if "inputRDI" in d:
        registres["inputRDI"] = d["inputRDI"]
    if "inputRSI" in d:
        registres["inputRSI"] = d["inputRSI"]

    print("Solution: ", )
    print("RDI: ", registres["inputRDI"])
    print("RSI: ", registres["inputRSI"])
    input("PAUSE...")
    
    shellcode = b''


taille =  int.from_bytes(p.recv(8), byteorder='little', signed=True)
print("last_len: ",taille)
shellcode = b''
while(len(shellcode)<taille):
    shellcode = shellcode+p.recv(0x1000)
print(shellcode) # flag in it :)

Bonus

Miasm have a DSE too, here an example (always with the Chaussette challenge):

from miasm.analysis.binary import Container
from miasm.analysis.machine import Machine
from miasm.core.locationdb import LocationDB
from miasm.jitter.csts import PAGE_READ, PAGE_WRITE,PAGE_EXEC
from miasm.analysis.dse import DSEPathConstraint
from miasm.expression.expression import ExprId, ExprInt, ExprAssign
import z3

def finish(jitter):
    print("Finished !")
    jitter.running = False
    return False

def solve_shellcode_dse_miasm(shellcode,run_addr):
    loc_db = LocationDB()

    cont = Container.from_string(shellcode, loc_db)
    machine = Machine("x86_64")
    mdis = machine.dis_engine(cont.bin_stream, loc_db=loc_db)
    myjit = machine.jitter(loc_db)


    myjit.vm.add_memory_page(run_addr, PAGE_READ | PAGE_WRITE | PAGE_EXEC, shellcode)
    myjit.init_stack()
    myjit.push_uint64_t(0xdead0000)

    myjit.add_breakpoint(0xdead0000, finish)

    myjit.init_run(run_addr)
    myjit.jit.log_regs = True
    myjit.jit.log_mn = True

    dse = DSEPathConstraint(machine, loc_db)
    regs = dse.ir_arch.arch.regs
    dse.attach(myjit) # we attach the dse to the jitter, now, every implemented instruction executed will now be symbolized.
    
    dse.update_state_from_concrete() # Synchronize the dse with jitter
    
    arg1 = ExprId("ARG", 64) # the name and the bit size
    arg2 = ExprId("ARG2", 64)

    RDI = ExprId("RDI", 64) # real registers from the shellcode (plain maj)
    RSI = ExprId("RSI", 64)

    dse.update_state({
        RDI: arg1,
        RSI: arg2
    })

    myjit.continue_run() # run until ret 

    result = dse.eval_expr(regs.RAX)

    condition0 = ExprAssign(result, ExprInt(0, 64)) # same as above

    dse.cur_solver.add(dse.z3_trans.from_expr(condition0)) # use z3 (so this will not work in Chaussette)

    assert dse.cur_solver.check() == z3.sat
    model = dse.cur_solver.model()

    for i, _ in enumerate(model):
        print(_, hex(model[_].as_long()))
    return model

Conclusion

Nice challenge which allows you to take a look at the tools available for this type of challenge.

Only problem: We haven’t yet encountered the fact of having to symbolize branches (the challenge is only one gigantic basic block). While it is an important part, in fuzzing in particular. We’ll see that later.